EN VOL - Comprendre la polaire pour mieux voler
- Détails
- Publication : dimanche 18 mai 2008 14:52
- Écrit par Jim

Pendant dix-huit années d'administration des tests pratiques de la FAA (NDLR: Federal Aviation Administration), j'ai réalisé que de nombreux pilotes de planeur et certains instructeurs de vol n'étaient pas du tout à l'aise avec la notion de courbe polaire. Si les graphiques vous embrouillent l'esprit, peut-être l'explication suivante vous sera utile.
Supposons que nous ayons quatre planeurs identiques, sauf pour la couleur. Pour notre test, nous les faisons partir au même endroit et les faisons voler à différentes vitesses qui impliquent différents taux de chute:
| Planeur | bleu | vert | jaune | rouge |
|---|---|---|---|---|
| Vitesse (km/h) | 48 | 57 | 78 | 115 |
| Taux de chute (m/s) | 0.9 | 0.8 | 1 | 1.7 |
Les quatre planeurs partent en même temps dans la même direction à leur vitesse et taux de chute respectif. Après une minute, leurs positions par rapport à leurs points de départ est la suivante :

Maintenant, si on connecte les planeurs par une courbe que l'on remplace sur le graph l'axe de distance par celui de la vitesse, on vient de tracer une courbe de polaire pour planeur en question.

Que peut-on tirer de la polaire ?
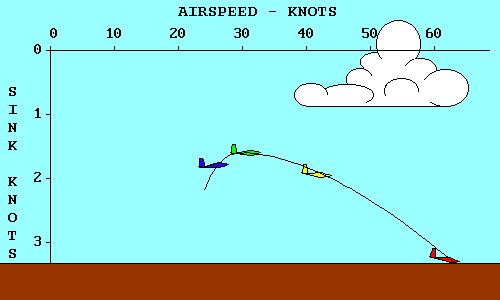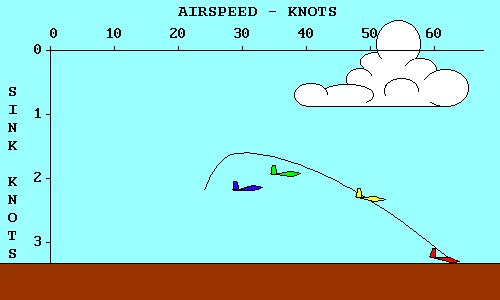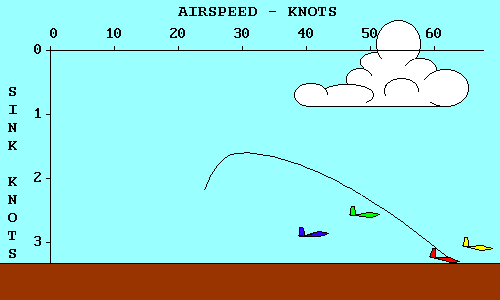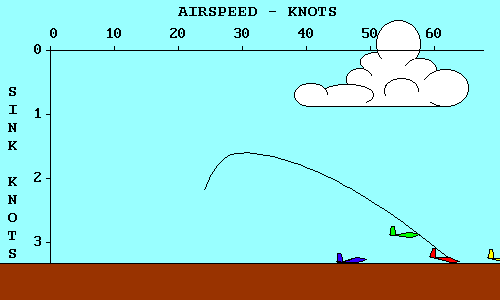
Le planeur vert a le plus faible taux de chute de tous. C'est celui qui vous tiendra en l'air le plus longtemps, mais vous ne pourrez pas aller loin. Notez que sa trajectoire coupe la polaire en son point le plus élevé. En reportant ce point sur l'axe horizontal de la vitesse, on peut savoir à quelle vitesse il faut aller pour bénéficier un taux de chute minimum (ici: 31 noeuds = 57 km/h)
En reportant le même point sur l'axe vertical, on apprend que son taux de chute mini est de 0.8 m/s (1,6 noeuds)

Le planeur jaune a la meilleurs finesse. Cela signifie qu'en air calme il volera plus loin que les autres pour une dénivellation donnée.
La droite qui passe par le point O,O (l'origine) du graph et qui est tangeante à la polaire représente le chemin du planeur jaune. Si l'on reporte le point de contact sur l'axe horizontal, on apprend que la vitesse avec laquel le planeur a la meilleure finesse (le plus long plané) est de 78 km/h.
Si l'on reporte le même point sur l'axe vertical, on trouve le taux de chute correspondant. (1,9 noeuds = 1m/s)

Si l'air était toujours calme, c'est tout ce que nous aurions besoin de savoir sur les courbes polaires. La vitesse du taux de chute mini nous garderait dans les airs le plus longtemps possible et la vitesse de finesse max nous permettrait de parcourir la plus grande distance.
Heureusement pour les pilotes de planeur, l'air se déplace verticalement et horizontalement. Quand il monte plus vite que notre taux de chute en son sein, nous gagnons de l'altitude. Quand il descend, nous devons modifier la vitesse de finesse max pour optimiser le vol dans cette zone.
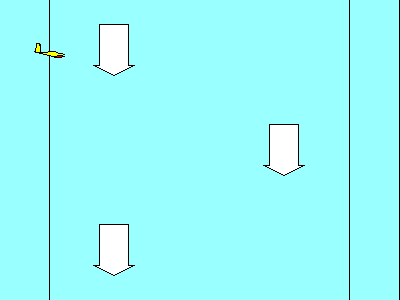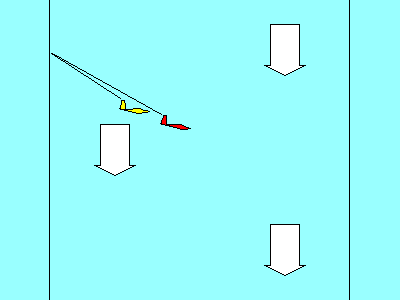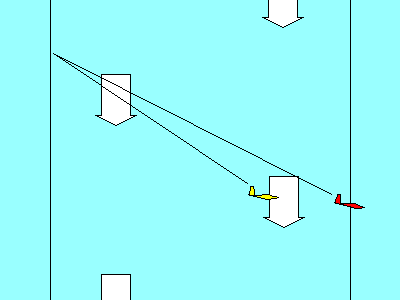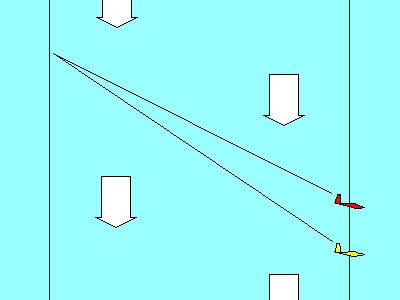
Pour voir comment l'air descendant affecte notre plané, comparons le planeur rouge et le jaune. Si les deux entrent dans une masse d'air qui s'enfonce à 1.5 m/s, leur taux de chute va augmenter de cette valeur. Le taux de chute du jaune est donc finalement de 2,5 m/s (1+1,5). Le taux de chute du planeur rouge se retrouve à 3,2 m/s (1,7+1,5)
Les deux entrant dans la masse d'air à la même altitude, l'objectif est de sortir l'autre côté avec le moins de perte d'altitude. Bien que le planeur rouge s'enfonce plus vite, il a également un déplacement horizontal beaucoup plus rapide (115 contre 78 km/h). Le résultat est qu'il sort de la zone d'air descendant à une altitude plus élevée que le planeur jaune. Le planeur rouge a une meilleure finesse par rapport au sol que le jaune, même si le planeur jaune a une meilleure finesse par rapport à la masse d'air.
Vous avez sans doute remarqué que les vitesses de ces planeurs n'ont pas été choisies au hasard. Le vert vol à la vitesse du taux de chute mini, le jaune à la vitesse qui donne la meilleure finesse en air calme et le rouge à la vitesse qui donne la meilleure finesse en air descendant à 1,5 m/s.
A présent, voyons comment on peut déterminer la vitesse de la finesse max pour toute masse d'air descendante.
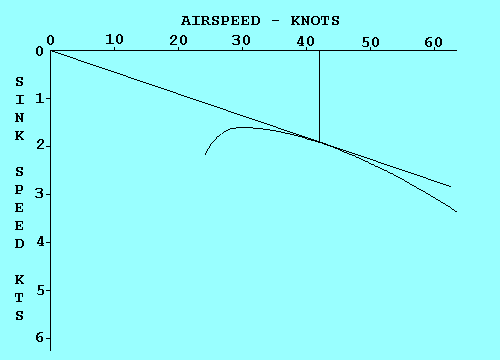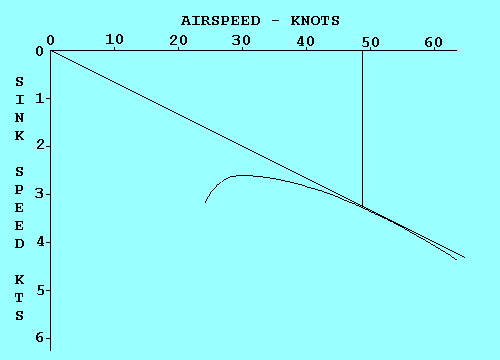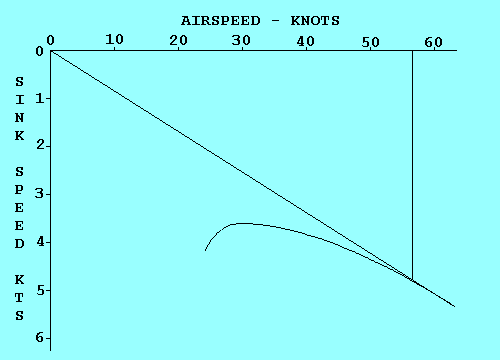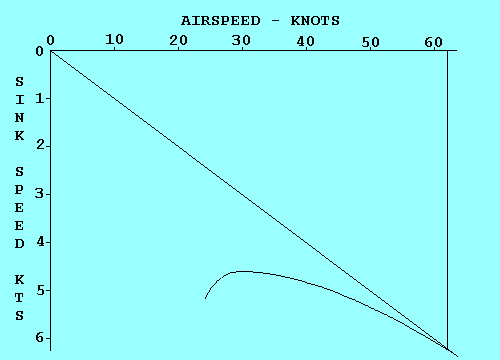
Si vous étiez en train de déterminer la vitesse optimale sur une polaire dessinée sur une feuille de papier, vous trouveriez très embêtant de devoir redessiner la polaire pour chaque vitesse d'air descendant...
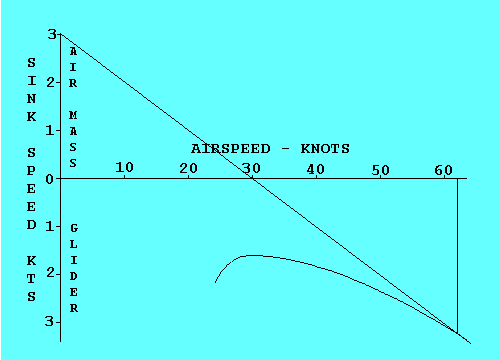
Une façon d'accomplir le même objectif est de faire monter l'origine du graph d'une valeur égale au taux de chute de la masse d'air, puis de tracer la tangeante.
On peut utiliser la même technique pour déterminer la vitesse optimale pour tout déplacement de la masse d'air.

Si la masse d'air est ascendante, on déplace l'origine le long de l'axe vertical d'une valeur égale au taux de montée de cette masse d'air. En traçasnt la tangeante passant par ce point, on trouve la vitesse optimale si l'on désire voler tout droit à travers le thermique. Si l'on désire enrouler la pompe, d'autres facteurs déterminent la vitesse à adopter pour monter le mieux possible.
Pour un vent de face, on déplace l'originevers la droite, pour un "vent de cul" , on déplace l'origine vers la gauche.
Il est également possible de combiner des mouvements de masses d'air. L'exemple montre comment procéder dans le cas où l'on se trouve dans un air descendant avec le vent de face.
Vous devez penser: "Tout cela est très intéressant, mais comment est-ce que j'utilise cette théorie en l'air ? Je ne vais pas aller voler avec mes graphs de polaire et tracer des tangeantes pour chaque condition que je rencontre..." Vous avez raison!
Il peut être fort utile de convertir ces informations sur un écran du tableau de bord ou de se créer une règle facile à retenir:
En ce qui concerne le vent de face et le vent "de cul". Si vous deviez analyser différentes conditions de vent graphiquement, vous vous apercevriez que le point de tangence se déplace de la moitié que l'origine. Une bonne règle serait de se rappeler: "Ajoute à peu près la moitié de la valeur du vent de face et soustrais à peu près la moitié de la valeur du vent "de cul" à la vitesse déterminée pour vent ascendant ou descendant.
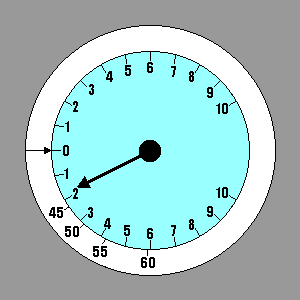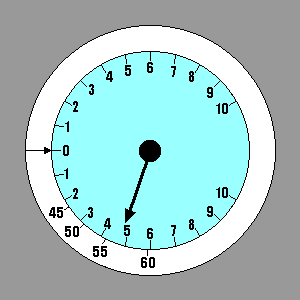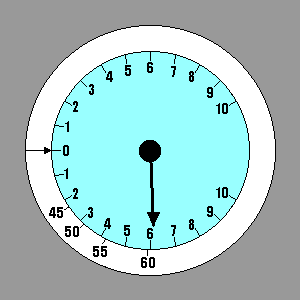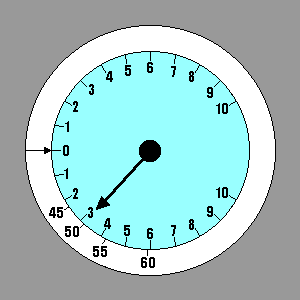
En ce qui concerne le vent ascendant et descendant, nous avons un instrument qui nous donne l'information nécessaire: le variomètre. Le processus utilisé pour déterminer la vitesse à laquelle il faut voler nous donne le taux de chute de la masse d'air et le taux de chute du planeur dans la masse d'air. Leur total est la valeur qui serait indiquée sur le variomètre. Nous pourrions sélectionner quelques valeurs représentatives des vitesses de vol et les indiquer sur le variomètre en utilisant une étiquette.
- - - - - - EN COURS DE TRADUCTION - - - - - - -
| For lift and sink we have an instrument in the glider to give us the necessary information. The process used to determine Speed to Fly gives us the sink rate of the air mass and the sink rate of the glider within the air mass. Their total is the value that would be indicated on the variometer. We could select a few representative values of Speed to Fly and stick them on the panel adjacent to the corresponding variometer readings, using a label maker. A better method is to invest in a speed ring for the glider/variometer combination we have. The speed ring is adjustable, but for our current definition of Speed to Fly it should be set with the arrow on the ring pointing to "0" on the variometer. Then when the variometer points to any rate of descent it is also pointing to the corresponding Speed to Fly - the one that will produce the flattest glide under those conditions. Our example shows Speed to Fly varying from 42 kts in still air to 62 kts in 3 kt sink. |
Bien que les vitesses de vol dont nous venons de parler sont celles qui sont idéales pour par exemple planer le mieux possible pour atteindre un terrain d'aterrissage, elles sont trop lentes pour vous faire gagner un concours de cross-country. Dans ce cas nous sommes plus intéressé à avancer le plus vite possible par rapport au sol en moins de temps possible qu'à obtenir la meilleure finesse. Cette notion introduit donc une nouvelle définition de la vitesses optimale...

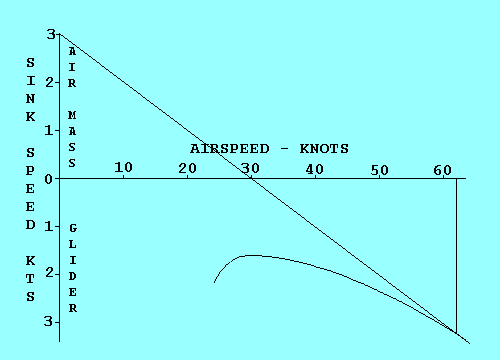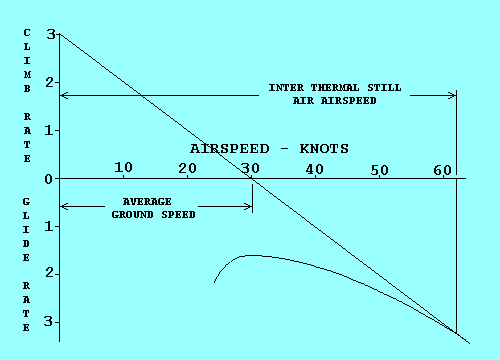
| We can analyze Speed to Fly in this case by using the same technique we used for flattest glide in sinking air, except that we offset the polar curve origin by the rate of climb we expect in the next thermal instead of air mass sink rate. To illustrate the similarity we assume a climb rate of 3 kts and see that the graph is identical to the one with 3 kts sink except for the labels. It shows that the Speed to Fly between thermals in still air is 62 kts if you expect to climb at 3 kts in the next thermal. An added benefit is that the average cross-country speed, including the time spent circling in thermals, can be estimated by the point on the airspeed scale where the tangent line crosses the scale. |
Now we see why the speed ring can be rotated about the variometer. If we expect our climb rate to be 3 kts, we set the arrow on the ring opposite where the vario indicates 3 kts climb. Note that the Speeds to Fly also move so that a higher speed is indicated for all sink rates. In this example the Speed to Fly in still air is 62 kts, just as the graph predicted. The sink rate in still air at this speed is 3.2 kts, as it has been for the red glider throughout this analysis.

| Some pilots might question using a climb rate in the next thermal, one that has not yet been attained, to set the speed ring. They should try to remember the last time they made a decision with complete information. In this case one could base the estimate on the climb rate in the last thermal, modified by an assessment of conditions ahead and whether they appear to be improving or deteriorating. Once set, the value selected is still subject to change. A good way to think of the MacCready setting is that it represents the minimum climb rate that the pilot is willing to stop for. As altitude decreases and the prospects of landing out increase, the prudent pilot will accept weaker thermals, and the MacCready ring should be set accordingly. A really desperate pilot should set the ring to zero to maximize the area to be searched for a thermal. |
The performance data used here is based on a SGS 1-26 at 575 pounds gross weight, as shown in Appendix A, The Joy of Soaring.

Merci à Jim pour la permission de traduction et diffusion
Traduit par Nicolas Vuille pour Wikidelta.com











